Research Project - Slowness as a computational principle for the visual cortex

The slowness principle

How does the brain process the sensory information? Is it possible to explain the activity and self-organization of the cortex by a single computational principle?

The work hypothesis of this project assumes that the cortex adapts itself in order to make the response of the neurons vary slowly in time. This is motivated by a simple observation: while the environment vary on a relatively slow timescale, the sensory input, e.g. in our case the response of receptors on the retina, consists of raw direct measurements that are very sensitive even to small transformations of the environment or the state of the observer. For example, a small translation or rotation of an object in the visual scene can lead to a dramatic change of the light intensity at a particular position of the retina. The sensory signal vary thus on a faster timescale than the environment. The work hypothesis implies that the cortex is actively extracting slow signals out of its fast input in order to recover the information about the environment and to build up a consistent internal representation. This principle is called the slowness principle.

Methods and results

We have chosen to approach this principle in a very direct way: we consider a large abstract set of functions and extract the ones that applied to sequences of natural images have the most slowly varying output (as measured by the mean of the squared derivative). This problem can be solved using Slow Feature Analysis (SFA) [1], an unsupervised algorithm based on an eigenvector approach (click here for a short description and literature about SFA).

This approach has the advantage of being independent from the actual neural architecture (since each extracted function can in principle be computed by many different neural circuits), so that we don't have to make additional assumptions about how the cortex work. Of course, we still have to choose an appropriate function space. Ideally, one would choose a very large function space. This is however not always possible in practice due to computational constraints. In our simulations we consider usually the set of all polynomials of degree two, which is still much larger than the function space spanned by the neural networks considered in related works [2,3] (simulations using other function spaces are work in progress).

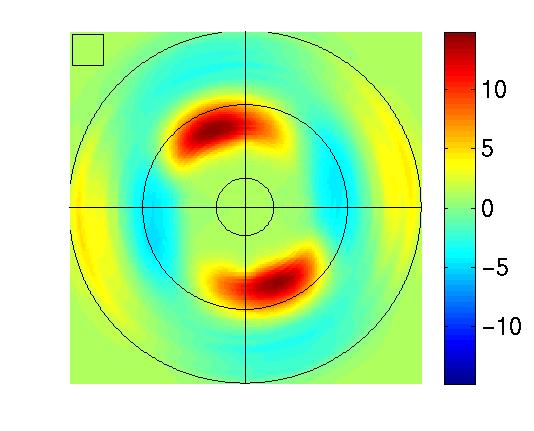
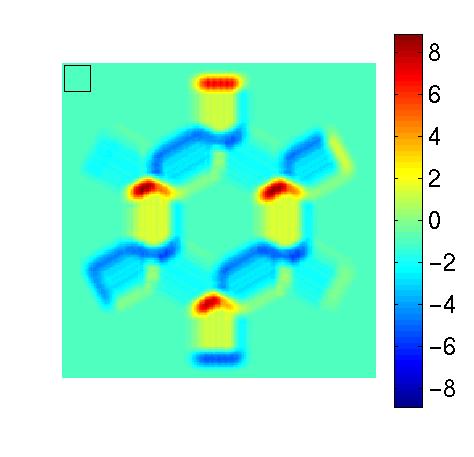
If the slowness hypothesis holds, cortical neurons compute slowly varying function. Their behavior should thus be equivalent to that of the functions extracted in our simulations. We study the characteristics of the functions in a way similar to the physiological experiments on V1, and compute the preferred input stimuli, their invariances and their response in a wide range of situations (Figure 1).

The results show that the extracted functions have many properties in common with complex cells in V1, including phase shift invariance, direction selectivity, non-orthogonal inhibition, end-inhibition and side-inhibition [4,5].

Additional material

The following pages contain additional informations, results and statistics relative to some simulations:

Index page of the research project.
Additional material to P.Berkes, L.Wiskott (2005), "Slow feature analysis yields a rich repertoire of complex cell properties", Journal of Vision 5(6), 579-602, http://journalofvision.org/5/6/9/.
Additional material to P.Berkes, L.Wiskott (2002), "Applying Slow Feature Analysis to image sequences yields a rich repertoire of complex cells properties", in "Artificial Neural Networks", Proceedings ICANN 2002, pp. 81-86 , Springer.

Figure 1, Example analysis of a slow function: a) Optimal excitatory stimulus (S+) (top) and optimal inhibitory stimulus (S-) (bottom). They correspond to the stimuli that elicit in the considered function the highest and the lowest response, respectively. b) Two invariances of the optimal excitatory stimulus shown in a) (top: phase-shift invariance, bottom: curvature invariance). Each frame shown is a nearly-optimal input stimulus to which the function responds with more than 80% of the optimal response (*). c) Test images. We use the top image to test the response of the functions to all orientation and to a range of frequencies. We use test images similar to the bottom one to study end- and side-inhibition: a function selective for the length- or width-extension of the input stimulus has a higher response on the borders of the hexagon than in its inner. The hexagonal shape is set to the preferred orientation and frequency of the considered function. d) Response images. The response images display the output of the function applied to each point of the corresponding test image. In the top image one can thus read to which range of orientation and frequencies the function respond strongly (red) or is inhibited (blue). The bottom image shows the response of a strongly end-inhibited function to the hexagonal test image shown in c). (As the function considered in the previous subfigures is not end-inhibited, we used here another one.) (Click on the response images to enlarge them.)

(*) If your browser fails to show the invariances in column b) as looping animations, please reload the page or open the images one by one (e.g. in "Netscape" or "Mozilla" right-click and select "View Image").

[1] L.Wiskott, T.Sejnowski, "Slow feature analysis: Unsupervised learning of invariances.", Neural computation, 14(4):715-770, 2002.

[2] C.Kayser, W.Einhäuser, O.Dümmer, P.König and K.P.Körding, "Extracting slow subspaces from natural videos leads to complex cells.", in "Artificial Neural Networks", Proceedings ICANN 2001, pp. 1075-1080, Springer 2001.

[3] A.Hyvärinen, P.Hoyer, "Emergence of phase and shift invariant features by decomposition of natural images into independent features subspaces", Neural Computation, 12(7): 1705-1720, 2000.

[4] P.Berkes, L.Wiskott, "Applying Slow Feature Analysis to image sequences yields a rich repertoire of complex cells properties", in "Artificial Neural Networks", Proceedings ICANN 2002, pp. 81-86 , Springer 2002.

[5] P.Berkes, L.Wiskott, "Slow feature analysis yields a rich repertoire of complex cell properties", Journal of Vision 5(6), 579-602, http://journalofvision.org/5/6/9/, 2005.

slowness project index page