The convergence of TD(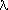 ) for general
) for general 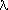 .
.
Peter Dayan
Machine Learning, 8, 341-362.
Abstract
The method of temporal differences (TD) is one way of making
consistent predictions about the future. This paper uses some analysis of
Watkins (1989) to extend a convergence theorem due to Sutton (1988) from
the case which only uses information from adjacent time steps to that
involving information from arbitrary ones. It also considers how this
version of TD behaves in the face of linearly dependent representations
for states-demonstrating that it still converges, but to a different
answer from the least mean squares algorithm. Finally it adapts Watkins'
theorem that Q-learning converges with probability one, to demonstrate
this strong form of convergence for a slightly modified version of TD.
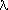 ) for general
) for general 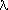 .
.
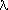 ) for general
) for general 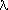 .
.