Bayesian Approaches
to Distribution Regression

Oxford
Gatsby unit, UCL
Oxford
Imperial College London

arXiv:1705.04293

Learning on Distributions, Functions, Graphs and Groups
NIPS 2017 \newcommand{\bP}{\mathbb{P}} \newcommand{\Xb}{\mathbf{X}} \newcommand{\X}{\mathcal{X}} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\N}{\mathcal N} \newcommand{\h}{\mathcal H} \newcommand{\u}{\mathbf u} \newcommand{\z}{\mathbf z} \newcommand{\R}{\mathbb R} \newcommand{\test}{\mathrm{test}} \newcommand{\tp}{^\mathsf{T}}

Distribution regression

-0.856
0.562
1.39

Labels y_i = f(\bP_i) Observe \Xb_i \stackrel{iid}{\sim} \bP_i Model \hat y_i = f(\Xb_i)

Different numbers of samples N_i

Distribution regression applications

  • “JIT” regression for EP messages [Jitkrittum+ UAI-15]
  • Choose summary statistics for ABC [Mitrovic+ ICML-16]
  • Infer demographic voting behavior [Flaxman+ KDD-15, 2016]
  • Galaxy cluster mass from velocities [Ntampaka+ ApJ 2015/2016]
  • Red shift estimation from galaxy clusters [Zaheer+ NIPS-17]
  • Model radioactive isotope behavior [Jin+ NSS-16]
  • Predict grape yields from vineyard images [Wang+ ICML-14]
  • …
  • (Plus lots of classification, anomaly detection, etc)

Distribution regression with kernel mean embeddings

  • Standard approach [e.g. Muandet+ NIPS 2012]
  • Choose RKHS \h with kernel k(x, y) = \langle \varphi(x), \varphi(y) \rangle_\h
    • e.g. k(x, y) = \exp\left( - \frac{1}{2 \sigma^2} \lVert x - y \rVert^2 \right)
  • Use mean embedding \mu_\bP = \E_\bP \varphi(X)
    • Reproducing property: for f \in \h , \langle f, \mu_\bP \rangle = \E_\bP \langle f, \varphi(X) \rangle_\h = \E_\bP f(X)
  • Mean embeddings are good representation for regression

Estimating kernel mean embeddings

  • \mu_\bP = \E_{X \sim \bP}\left[ \varphi(X) \right] \in \h is a good summary of \bP
  • But don't know \mu_\test or \bP_\test ; just have N_\test samples
  • Natural estimate: empirical mean
    • \hat\mu_\bP = \frac{1}{N} \sum_{j=1}^N \varphi(x_j)
  • Inner products:
    • \langle \hat\mu_1, \hat\mu_2 \rangle_\h = \frac{1}{N_1 N_2} \sum_{i=1}^{N_1} \sum_{j=1}^{N_2} k(x^1_i, x^2_j)
  • But…point estimate worse for small N_i

Posterior for mean embeddings [Flaxman+ UAI 2016]

  • Place prior: \mu_i \sim \mathcal{GP}(m_0, r(\cdot, \cdot))
  • Likelihood is “observed” at points \u : \hat\mu_i(\u) \mid \mu_i(\u) \sim \N(\mu_i(\u), \Sigma_i / N_i)
  • Get a closed-form GP posterior for \hat\mu_i \mid \Xb_i : \begin{align} \mu_i(\z&) \mid \Xb_i \sim \N\biggl( \\& R_{\z \u} (R_{\u\u} + \Sigma_i / N_i)^{-1} (\hat\mu_i - m_0) + m_0, \\& R_{\z \z} - R_{\z\u} (R_{\u\u} + \Sigma_i / N_i)^{-1} R_{\u\z} \biggr) \end{align}
  • Mean matches Stein shrinkage estimator [Muandet+ ICML 2014]

Distribution regression with kernel mean embeddings

  • Model label as function of mean embedding: \begin{align} y_\test = f^*(\mu_\test) + \varepsilon \end{align}
  • Estimate with ridge regression: \begin{align} \hat y_\test &= f(\hat\mu_\test) = \sum_{i=1}^n \alpha_i \langle \hat\mu_\test, \hat\mu_i \rangle_\h \end{align}
  • Landmark approximation: f(\hat\mu) = \beta\tp \hat\mu(\u) = \sum_{\ell=1}^s \beta_\ell \hat\mu(u_\ell)
  • Have uncertainty about both \beta and \hat\mu

Shrinkage model

  • Uses [Flaxman+ UAI 2016]'s GP posterior for \mu_i \mid \Xb_i
  • Point estimate for weights \beta
  • Observations y_i \mid (\mu_i, f) \sim \N\left( \langle f, \mu_i \rangle_\h, \sigma^2 \right)
  • Landmark approximation: f(x) = \sum_{\ell=1}^s \beta_\ell k(x, z_\ell)
  • Get y_i \mid (\Xb_i, \beta, \z) \sim \N(\xi_i^\beta, \nu_i^\beta)
  • Can get MAP estimate for \beta , \sigma , kernel params, …

Bayesian linear regression

  • Assumes \mu are known exactly: point estimate at \hat\mu
  • Regression weight uncertainty: \beta \sim \N(0, \rho^2)
  • Observations: y_i \mid (\mu_i, \beta) \sim \N(\beta\tp \hat\mu_i(\u), \sigma^2)
  • Posterior for y_i \mid \Xb_i is normal
    • Hyperparameters: \sigma , \rho , kernel params…

Full Bayesian Distribution Regression

  • Shrinkage posterior for \mu_i \mid \Xb_i
  • Normal model for regression weights: \beta \sim \N(0, \rho^2)
  • Observations y_i \mid (\mu_i, f) \sim \N\left( \beta\tp \mu_i(\u), \sigma^2 \right)
  • \beta is non-conjugate; MCMC inference with Stan

Models recap

Model \mu \beta Inference
ShrinkageGP modelpoint est.conjugate+MAP
BLRpoint est.normalconjugate+MAP
BDRGP modelnormalconjugate+MCMC

Toy experiment

  • Labels y_i uniform over [4, 8]
  • 5d data points: \left[x^i_j\right]_\ell \mid y_i \stackrel{iid}{\sim} \frac{1}{y_i} \Gamma\left(\frac{y_i}{2}, \frac12 \right)

(s_5, 25, 25, 100-s_5)\% have N_i = (5, 20, 100, 1000)

Toy experiment: NLL

BDR \approx shrinkage < BLR in NLL:

Toy experiment results: MSE

Same BDR \approx shrinkage < BLR in MSE. (Predicting mean: 1.3)

Toy experiment

  • Variant with constant N_i , added noise:
  • BDR \approx BLR < shrinkage in NLL, MSE
  • BDR can take advantage of both situations

Age prediction from face images

\Biggl\{ , , , , \Biggr\} \to 35

IMDb database [Rothe+ 2015]: 400k images of 20k celebrities

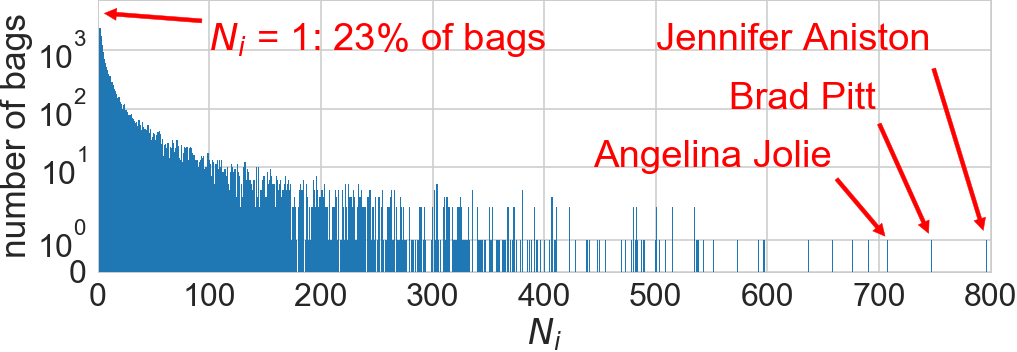
Age prediction results

Features: last hidden layer of Rothe et al.'s CNN

Shrinkage really helps!

Recap

Three Bayesian models for distribution regression:

Model \mu \beta Inference
ShrinkageGP modelpoint est.conjugate+MAP
BLRpoint est.normalconjugate+MAP
BDRGP modelnormalconjugate+MCMC
  • Both kinds of uncertainty can help
  • BDR can take advantage of both settings

Bayesian Approaches to Distribution Regression

Ho Chung Leon Law, Dougal J. Sutherland, Dino Sejdinovic, Seth Flaxman

arXiv:1705.04293