Research

---

More than a century’s worth of behavioural investigations have demonstrated that animals and humans process sensory information close to optimally, often employing subtle and powerful algorithms to do so. Our understanding of these computations at the neural level is, by contrast, quite simplistic. The goal of research in my group is to help bridge this gap, using both theoretical and data-driven approaches to understand how information is represented in neural systems, and how this representation underlies computation and learning. On the one hand, we collaborate closely with physiologists to advance the technology of neural data collection and analysis. These studies have the potential to introduce powerful new theoretically-motivated ways of looking at neural data. At the same time, we examine neural information representation and perceptual behaviour from a more theoretical point of view, addressing questions of how the brain might encode the richness of information needed to explain perceptual capabilities, what purpose might be served by adaptation in neural activities, and how experience-driven plasticity in representations is related to perceptual learning. Both the data analytic and the theoretical aspects of our neuroscience research are closely connected to the field of machine learning, which provides the tools needed for the first, and a structural framework for the second.

Current and Recent Projects

Theoretical Neuroscience

Theoretical research in my group is built around a key idea in modern theoretical neuroscience: that the act of perception is a search for the causal elements most likely to account for the activity of the sensory epithelia. This ”statistical inference” hypothesis, traceable to the work of von Helmholtz and before, has far-reaching consequences for the way we study and think about brain function, and work in my group has explored many of its different facets.

• The statistics of the sensory environment

  If perception does indeed proceed by statistical inference, the brain must embody knowledge of the statistical causal structure of the natural environment. We seek to discover this structure, using the methods of probabilistic unsupervised learning to build statistical models of natural stimuli, and drawing parallels between the elements of such models and neural processing and behaviour.

  • Many statistical models of image data have relied on sparse models of static images or “slow” models of video. We have taken a probabilistic approach to both sparsity [33] and slowness [45]; and have synthesised them in a structured model for natural image sequences [25], which matches both the receptive field properties and anatomical grouping of cells in the visual cortex, and suggests a new interpretation of complex and simple cells properties as representing the presence and appearance respectively of visual features. We have also explore sparse image models with competitive or occlusive source interactions, rather than the conventional linear superposition. [26, 37, 43]. (With Pietro Berkes, Jörg Lücke, Richard Turner)

    

    Identity-Attribute models. A natural image can be characterised by a set of binary variables that indicate which objects appear, and a set of variables specifying attributes such as apparent size and rotation, which determine how they look. In the real world (left), this leads to a substantially nonlinear model. In our simplification (right, [25]) these nonlinearities are reduced to a single product. Despite this, the model captures essential elements of the structure of video.

  • Similar ideas should extend to sound, but here time must play an even more crucial role. We have studied the statistics of sound in both signal-processing [23, 44] and more natural [39] settings. Much of our work relies on the statistics of processes formed by a hierarchical cascade of modulators (With Richard Turner).
• Perception

  Much of our work focuses directly on perception, building probabilistic models of specific perceptual processes—in some cases based on the statistical models derived above—and using these to understand human and animal behaviour. In many cases, these models make behavioural or psychophysical predictions that we are able to test experimentally.

  • Much of our understanding of perception as inference has relied on both analysis and experiments in relative simple settings—most often relying on perceptual reports about a single well-defined property. Many interesting perceptual phenomena arise only in more crowded or cluttered settings. We are interesting in modelling inference in such settings [15], and suspect that sensory attention may play a role in shaping inference under such conditions [4]. (With Louise Whiteley )
  • Statistically optimal perception requires that observers be able to build and use internal models of their sensory uncertainty. We have shown that observers can integrate internal estimates of uncertainty with externally-imposed loss functions to guide decisions [41], and—in a functional imaging collaboration with Ray Dolan’s laboratory—that this integration seems to take place at a late stage of decision making [22]. (With Louise Whiteley, Steve Fleming, Ray Dolan )
  • We have proposed a new model for the perception of elapsed time that depends on the integration of cues derived from temporal statistics in sensory input with internal estimates [9]. The model reproduces the scalar law of timing as well as previously known stimulus-induced timing biases, and is supported by the results of three new psychophysics experiments (see below). The underlying statistical model also provides a plausible hypothesis for neural (non-sensory) timekeeping [32]. (With Misha Ahrens )

    

    Random stimuli affect our sense of time. The figure shows five frames of the Gaussian noise stimuli we used in our experiments on timing [9]. Click on the image to view a movie of one such stimulus. You will see two segments of noise in succession, the first changing rapidly and the second more slowly. Both segments are of equal true length (video player permitting); in our controlled experiments, observers experienced the first as lasting longer.

  • Most recently, we have begun to study the perception of pitch, an attribute of sound that is surprisingly difficult to define. We have shown how apparently conflicting perceptual results may be reconciled by a view in which the percept of pitch is identified with the period derived from noisy model auditory nerve firing rates assuming a simple statistical model of pseudo-periodic waveform generation. (With Phillipp Hehrmann )
• Other themes

  We also have interests in the representation and manipulation of uncertainty by neural populations [58]; task-driven plasticity in primary sensory cortex [51]; sensory adaptation [55]; statistical outlier detection in the nervous system; and motor planning (in collaboration with the Neural Prosthetic Systems Laboratory at Stanford University).

Neural Data Modelling

Ultimately, any attempt to link theory to neural circuits will demand a sophisticated understanding of both representation and dynamics within real neural systems. Thus, the group maintains substantial collaborations with neurophysiologists. Our goals in these collaborations are both technological and scientific—developing the algorithms needed to make sense of the flood of neurophysiological data available, while at the same time gaining insight into representations and computations in the brain.

• Dynamics in neural populations

  Neurons coöperate in large interconnected populations to represent and process information. Technical limitations over the last many decades, however, have meant that almost all of what we know about neuronal processing has been based on inferences made from the activity of cells measured one at a time. Over the last five to ten years, the technology to monitor simultaneous activity in larger ensembles has been more widely adopted, and this new stream of data provides new opportunities and poses new challenges.

  Our approach to such data (in collaboration with Krishna Shenoy’s laboratory at Stanford and other groups in the DARPA REPAIR programme; [42]) rests on the idea the the collective activity of multiple cells in the same area can be described by the evolution of a smaller set of latent variables or “order parameters” that capture the dynamics of the network. We have worked on parametric techniques to identify linear or non-linear dynamics in such systems [13, 14, 47, 48], and more recently on Gaussian Process methods to identify underlying latent trajectories without constrained dynamics [28, 29, 35, 36]. Our approach has begun to yield new insight into the process of motor preparation [10] and dynamics within many different cortical areas [20]. (With Jakob Macke, Biljana Petreska, Alex Lerchner, Lars Büsing, Byron Yu, John Cunningham, Afsheen Afshar, Krishna Shenoy, and others at Stanford. )

• Neural encoding

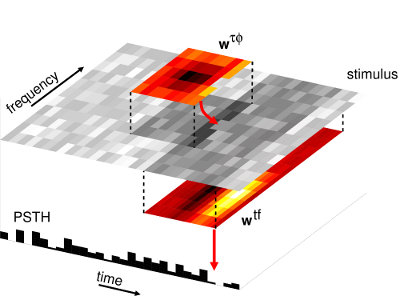
  A substantial current focus in auditory research is on understanding representation at the first cortical stages of the auditory pathway. By building models of how cells in the primary auditory cortex respond to stimuli, Jennifer Linden (UCL Ear Institute) and I hope to understand the function of these cortical areas, and how that function is affected by acoustic context and auditory learning. In early work we looked at the standard models for central auditory responses—called spectro-temporal receptive fields (STRFs)—and developed methods both to improve the fidelity with which they might be estimated, and to measure their predictive quality [59, 60]. The conclusion was that the best-fit model could capture no more than 30% of the predictable variance in the response. This discovery has led us to question the intepretation of STRF models [34]; and to build new nonlinear models that improve predictive performance [30, 31]. These latter models have now led to exciting new results, demonstrating that different cortical subfields have distinct nonlinear properties, and that auditory learning is associated with changes in nonlinear cortical processing. (With Misha Ahrens, Ross Williamson, Bjorn Christianson, and Jennifer Linden).

  

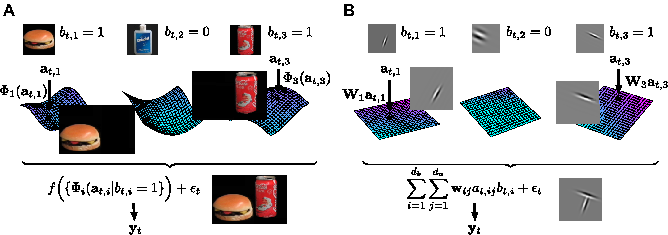
  The context model. This multilinear model [30] captures short-term context effects in the neural response to complex sounds.

  As simultaneous recordings from multiple neurons become more commonplace, we see the emphasis in experimental encoding studies moving from single cells to population-based methods. We have already begun to gather such multi-site data from the auditory cortex, and have also initiated new collaborations with two groups at UCL that are already collecting remarkably rich data sets in the visual cortex. Our collaboration with Matteo Carandini has begun by looking at interactions between neurons and local field potential recordings at sites regularly spaced across the visual cortex. At the same time, with Tom Mrsic-Flogel, we are beginning to look at calcium imaging data from a number of individual cells packed into a relatively small cortical region. In both cases, we hope to be able to use techniques and algorithms developed as part of our population dynamics models in motor areas to advance our understanding of sensory processing. (With Jakob Macke, David Schulz)

• Neural decoding

  At the other end of sensory-motor processing, the question of how neural activity encodes intended or current movements—and how this activity may be decoded to provide effective motor facilities in paralysed patients—is of considerable interest. Collaborating with the Shenoy group again, we have developed probabilistic methods for decoding [40], with a particular emphasis on combining information about both intended and current motor actions [24, 27, 38, 46, 56]. These algorithms are being implemented in real-time systems, with a view to clinical development, as part of the DARPA Revolutionising Prosthetics 2009 programme.

Machine Learning and Signal Processing

At the heart of our work lie the methods of probabilistic (or Bayesian) modelling, particularly as they apply to the fields of Machine Perception and Learning, and Signal Processing. Some of our work is directed more specifically at understanding and developing these tools.

• Approximation

  We are particularly interested in characterising the impact of the sorts of deterministic approximation often used to accelerate inference in Machine Learning applications. Particularly in time series, common approaches such as Laplace approximation, variational methods and EP introduce potential biases [17, 47], some of which may be counter-intuitive. As such methods have become a central element of the modelling toolbox, understanding these biases is of substantial importance.

• Sparsity

  Models with sparse priors play a major role in modern signal processing. We have developed a variety of probabilistic approaches to sparsity; exploiting hyperparameter optimisation [33, 52, 59] as well as sparse structures and approximate sparse search [37].

• Statistical signal processing

  Although probabilistic methods have played a notable role in extracting high-level information from signals such as sounds, they have been used less for lower-level signal representation and decomposition. We have developed new techniques for single- and multi-band amplitude and frequency demodulation [19, 18, 23, 39, 44], which address the fundamentally ill-posed nature of such problems from a Bayesian standpoint.

  

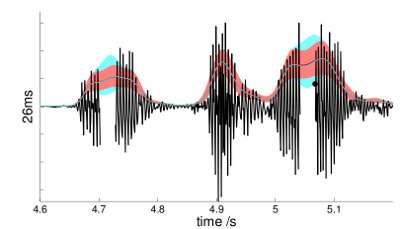
  Filling in the envelope of missing segments of a natural signal using PAD. The red line and region show the estimated envelope and posterior width using the complete signal; the cyan line and region are estimated from the signal with drop-outs.

• Dimensionality reduction

  Finally, our work on GPFA [28] reflects a more extensive interest in dimensionality reduction in the context of time-series data—a problem made complicated by uneven sampling and a desire for the simultaneous characterisation of the embedded manifold and a probabilistical account of the time-series evolution on that manifold.

Older work

My Ph.D. Thesis on Latent Variable Models for Neural Data Analysis is available from this page. It covers a range of statistical modelling and data analytic topics, including:

• Relaxation (annealing) schemes for EM and cascading (online) model order selection.
• Identification of spikes from different cells in extracellular recordings.
• Randomly-scaled poisson process models for stimulus-evoked spike trains.

I have also worked on

• MEG denoising and (correlated) source localization (with Srikantan Nagarajan) [52].
• Conditional entropy estimation in low-data categorical experiments.
• Online experimental design [poster].

A selected list of publications appears on the next page.