\definecolor{cb1}{RGB}{76,114,176} \definecolor{cb2}{RGB}{221,132,82} \definecolor{cb3}{RGB}{85,168,104} \definecolor{cb4}{RGB}{196,78,82} \definecolor{cb5}{RGB}{129,114,179} \definecolor{cb6}{RGB}{147,120,96} \definecolor{cb7}{RGB}{218,139,195} \newcommand{\cP}[1]{{\color{cb1} #1}} \newcommand{\PP}{\cP{\mathbb{P}}} \newcommand{\pp}{\cP{p}} \newcommand{\X}{\cP{X}} \newcommand{\Xp}{\cP{X'}} \newcommand{\cQ}[1]{{\color{cb2} #1}} \newcommand{\QQ}{\cQ{\mathbb Q}} \newcommand{\qq}{\cQ{q}} \newcommand{\Y}{\cQ{Y}} \newcommand{\Yp}{\cQ{Y'}} \newcommand{\vtheta}{\cQ{\theta}} \newcommand{\Qtheta}{\QQ_\vtheta} \newcommand{\qtheta}{\cQ{q}_\vtheta} \newcommand{\Gtheta}{G_\vtheta} \newcommand{\cZ}[1]{{\color{cb5} #1}} \newcommand{\Z}{\cZ{Z}} \newcommand{\ZZ}{\cZ{\mathbb Z}} \newcommand{\cpsi}[1]{{\color{cb3} #1}} \newcommand{\vpsi}{\cpsi{\psi}} \newcommand{\vPsi}{\cpsi{\Psi}} \newcommand{\Dpsi}{D_\vpsi} \newcommand{\fpsi}{f_\vpsi} \newcommand{\SS}{\cpsi{\mathbb{S}}} \newcommand{\Xtilde}{\cpsi{\tilde{X}}} \newcommand{\Xtildep}{\cpsi{\tilde{X'}}} \DeclareMathOperator{\D}{\mathcal{D}} \newcommand{\dom}{\mathcal X} \DeclareMathOperator*{\E}{\mathbb{E}} \newcommand{\F}{\mathcal{F}} \DeclareMathOperator{\ent}{H} \DeclareMathOperator{\JS}{JS} \DeclareMathOperator{\KL}{KL} \DeclareMathOperator{\ktop}{\mathit{k}_\mathrm{top}} \DeclareMathOperator{\mean}{mean} \DeclareMathOperator{\MMD}{MMD} \DeclareMathOperator{\MMDhat}{\widehat{MMD}} \newcommand{\lip}{\mathrm{Lip}} \newcommand{\optMMD}{\mathcal{D}_\mathrm{MMD}} \newcommand{\R}{\mathbb{R}} \newcommand{\tp}{^\mathsf{T}} \newcommand{\ud}{\mathrm{d}} \DeclareMathOperator{\W}{\mathcal{W}}

Generative Adversarial Networks

Dougal J. Sutherland
Gatsby, UCL→TTIC→UBC

(from thispersondoesnotexist.com)

MLCC 2019

(Swipe or arrow keys to move through slides; m for a menu to jump; ? to show more.)

Generative models

  • Start with a bunch of examples: \X_1, \dots, \X_n \sim \PP
  • Want a model for the data: \QQ \approx \PP
  • Might want to do different things with the model:
    • Find most representative data points / modes
    • Find outliers, anomalies, …
    • Discover underlying structure of the data
    • Impute missing values
    • Use as prior (semi-supervised, machine translation, …)
    • Produce “more samples”
    • …

Why produce samples?

Generative models: a traditional way

  • Maximum likelihood: \max_\vtheta \E_{\X \sim \PP}[ \log \qtheta(\X) ]
  • Equivalent: \min_\vtheta \KL(\PP \| \Qtheta) = \min_\vtheta \int \pp(x) \log \frac{\pp(x)}{\qtheta(x)} \ud x

Traditional models for images

  • 1987-style generative model of faces (Eigenface via Alex Egg)
  • Can do fancier versions, of course…
  • Usually based on Gaussian noise \approx L_2 loss

A hard case for traditional approaches

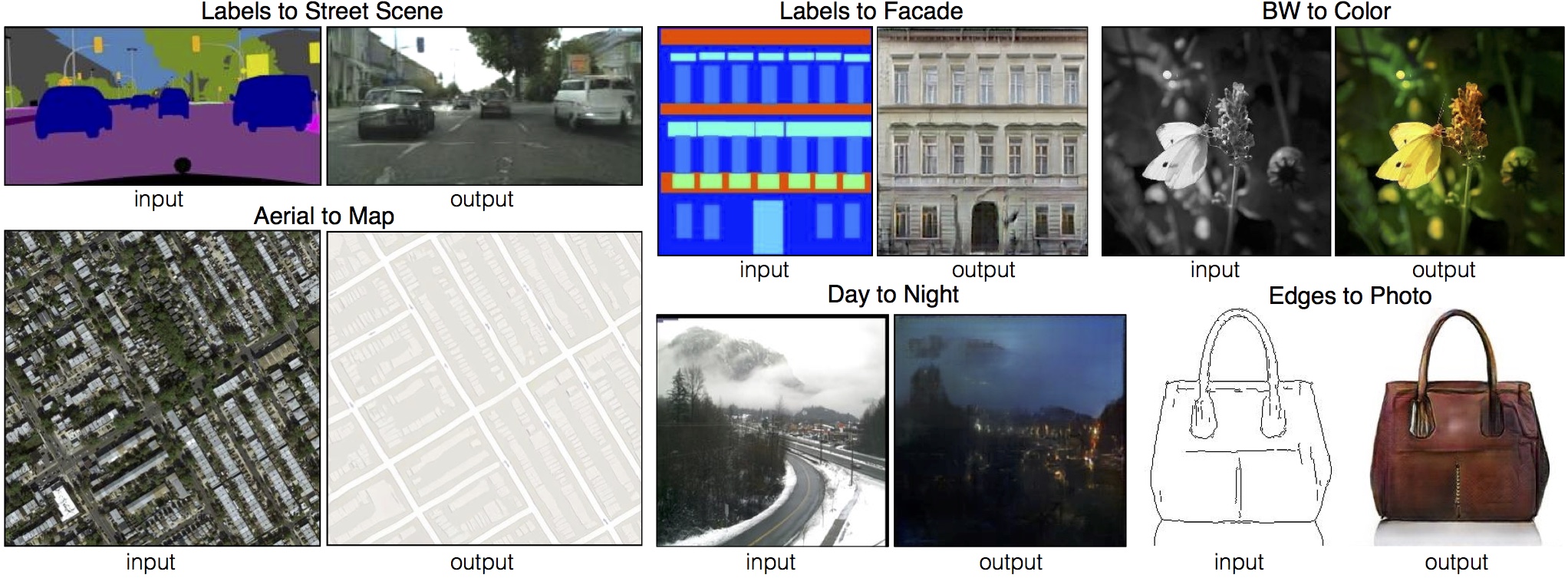
  • One use case of generative models is inpainting [Harry Yang]:
  • L_2 loss / Gaussians will pick the mean of possibilities

Next-frame video prediction

[Lotter+ 2016]

Trick a discriminator [Goodfellow+ NeurIPS-14]

Generator ( \Qtheta )

Discriminator

Target ( \PP )

Is this real?

No way! \Pr(\text{real}) = 0.03

:( I'll try harder…

⋮

Is this real?

Umm… \Pr(\text{real}) = 0.48

Aside: deep learning in one slide

  • MLCC so far: models f(x) = w\tp \Phi(x) + b , f : \mathcal X \to \R
  • \begin{align} f_0(x) &= x \\ f_{\ell}(x) &= \sigma_\ell\left( W_\ell f_{\ell - 1}(x) + b_\ell \right), f_\ell : \R^{d_{\ell - 1}} \to \R^{d_\ell} \end{align}
  • \sigma_\ell is an activation function:
    \max(x, 0) \qquad \frac{1}{1 + e^{- x}} \qquad \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} \qquad \cdots
  • Classification usually uses log loss (cross-entropy): \ell(y, t) = 1(t = 1) \log f(x) + 1(t = 0) \log(1 - f(x))
  • Optimize with gradient descent

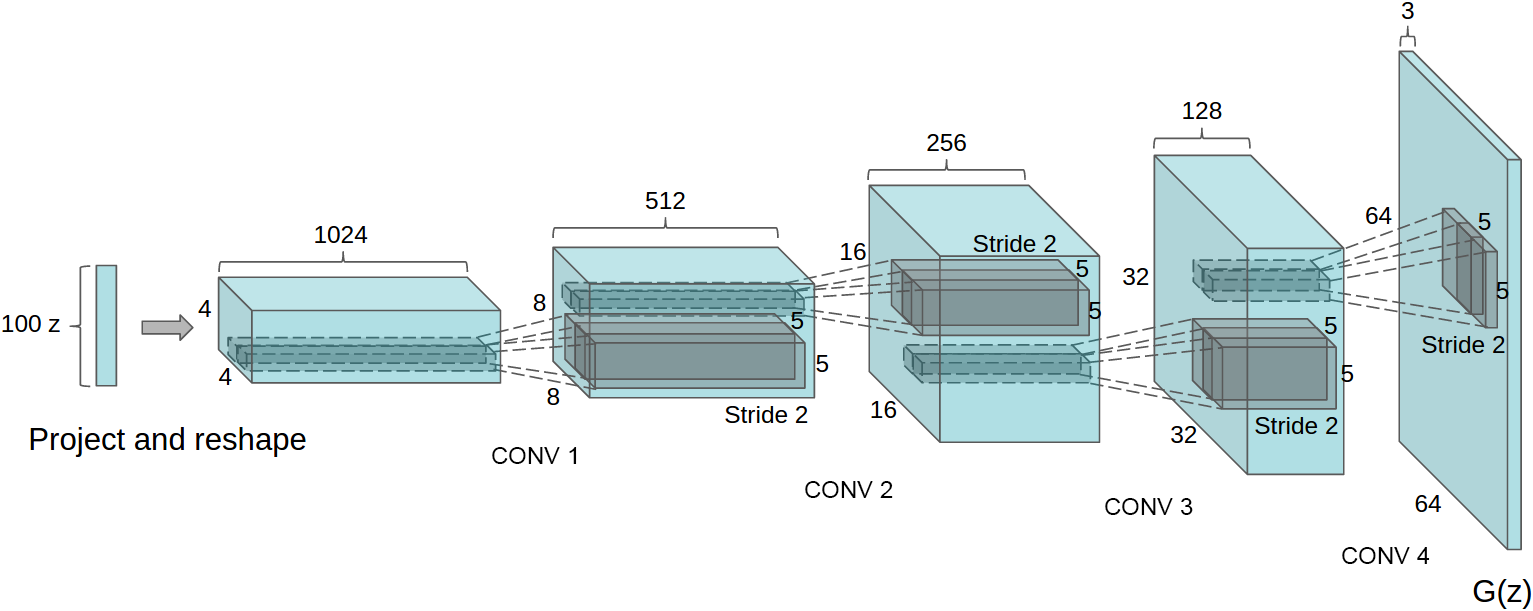
Generator networks

  • How to specify \Qtheta ?
  • \Z \sim \ZZ = \mathrm{Uniform}\left( [-1, 1]^{100} \right)
  • \Gtheta : [-1, 1]^{100} \to \dom , \Gtheta(\Z) \sim \Qtheta

GANs in equations

  • Tricking the discriminator: \min_\vtheta \max_\vpsi \tfrac12 \E_{\X \sim \PP}\left[ \log \Dpsi\!\left( \X \right) \right] + \tfrac12 \E_{\Y \sim \Qtheta}\left[ \log \left( 1 - \Dpsi\!\left( \Y \right) \right) \right]
  • Using the generator network for \Qtheta : \min_\vtheta \max_\vpsi \tfrac12 \E_{\X \sim \PP}\left[ \log \Dpsi\!\left( \X \right) \right] + \tfrac12 \E_{\Z \sim \ZZ}\left[ \log \left( 1 - \Dpsi\!\left( \Gtheta(\Z) \right) \right) \right]
  • Can do alternating gradient descent!

Original paper's results [Goodfellow+ NeurIPS-14]



DCGAN results [Radford+ ICLR-16]

Training instability

Running code from [Salimans+ NeurIPS-16]:

Run 1, epoch 1

Run 1, epoch 2

Run 1, epoch 3

Run 1, epoch 4

Run 1, epoch 5

Run 1, epoch 6

Run 1, epoch 11

Run 1, epoch 501

Run 1, epoch 900

Run 2, epoch 1

Run 2, epoch 2

Run 2, epoch 3

Run 2, epoch 4

Run 2, epoch 5

One view: distances between distributions

  • What happens when \Dpsi is at its optimum?
  • If distributions have densities, \Dpsi^*(x) = \frac{\pp(x)}{\pp(x) + \qtheta(x)}
  • If \Dpsi stays optimal throughout, \vtheta tries to minimize \!\!\!\! \frac12 \E_{\X \sim \PP}\left[ \log \frac{\pp(\X)}{\pp(\X) + \qtheta(\X)} \right] + \frac12 \E_{\Y \sim \Qtheta}\left[ \log \frac{\qtheta(\X)}{\pp(\X) + \qtheta(\X)} \right] which is \JS(\PP, \Qtheta) - \log 2

Jensen-Shannon divergence

\begin{align} \JS(\PP, \Qtheta) &= \frac12 \int \pp(x) \log \frac{\pp(x)}{\frac12 \pp(x) + \frac12 \qtheta(x)} \ud x \\&\quad + \frac12 \int \qtheta(x) \log \frac{\qtheta(x)}{\frac12 \pp(x) + \frac12 \qtheta(x)} \ud x \\&\fragment{{}= \frac12 \KL\left( \PP \,\middle\|\, \frac{\PP + \Qtheta}{2} \right) + \frac12 \KL\left( \Qtheta \,\middle\|\, \frac{\PP + \Qtheta}{2} \right) } \\&\fragment{{}= \ent\left[ \frac{\PP + \Qtheta}{2} \right] - \frac{\ent[\PP] + \ent[\Qtheta]}{2}} \end{align}

JS with disjoint support [Arjovsky/Bottou ICLR-17]

\begin{align} \JS(\PP, \Qtheta) &= \frac12 \int \pp(x) \log \frac{\pp(x)}{\frac12 \pp(x) + \frac12 \qtheta(x)} \ud x \\&+ \frac12 \int \qtheta(x) \log \frac{\qtheta(x)}{\frac12 \pp(x) + \frac12 \qtheta(x)} \ud x \end{align}

  • If \PP and \Qtheta have (almost) disjoint support \frac12 \int \pp(x) \log \frac{\pp(x)}{\frac12 \pp(x)} \ud x \fragment{= \frac12 \int \pp(x) \log(2) \ud x} \fragment{= \frac12 \log 2} so \JS(\PP, \Qtheta) = \log 2

Discriminator point of view

Generator ( \Qtheta )

Discriminator

Target ( \PP )

Is this real?

No way! \Pr(\text{real}) = 0.00

:( I don't know how to do any better…

How likely is disjoint support?

  • At initialization, pretty reasonable:
    \PP :
    \Qtheta :
  • Remember we might have \Gtheta : \R^{100} \to \R^{64 \times 64 \times 3}
  • For usual \Gtheta , \Qtheta is supported on a countable union of
    manifolds with dim \le 100
  • “Natural image manifold” usually considered low-dim
  • No chance that they'd align at init, so \JS(\PP, \Qtheta) = \log 2

A heuristic partial workaround

  • Original GANs almost never use the minimax game \min_\vtheta \max_\vpsi \tfrac12 \E_{\X \sim \PP}\left[ \log \Dpsi\!\left( \X \right) \right] + \tfrac12 \E_{\Y \sim \Qtheta}\left[ \log \left( 1 - \Dpsi\!\left( \Y \right) \right) \right]
  • \max_\vtheta \log \Dpsi(\Gtheta(\Z)), \text{ not } \min_\vtheta \log(1 - \Dpsi(\Gtheta(\Z)))
  • If \Dpsi is near-perfect, near \log 0 instead of \log 1
  • When \Dpsi is near-perfect, makes it unstable instead of stuck

Solution 1: the Wasserstein distance

\W(\PP, \QQ) = \sup_{f : \lVert f \rVert_\lip \le 1} \E_{\X \sim \PP}[f(\X)] - \E_{\Y \sim \QQ}[f(\Y)]

f : \dom \to \R is a 1 -Lipschitz critic function

\lVert f \rVert_\lip = \sup_{x, y \in \dom} \frac{\lvert f(x) - f(y) \rvert}{\lVert x - y \rVert} = \sup_{x \in \dom} \lVert \nabla f(x) \rVert

Turns out \W is continuous: if \Qtheta \to \PP , then \W(\Qtheta, \PP) \to 0

Wasserstein GANs

  • Idea: turn discriminator \Dpsi into a critic \fpsi
  • Need to enforce \lVert \fpsi \rVert_\lip \le 1
  • Easy ways to do this are way too stringent
  • Instead, control \lVert \nabla f(\Xtilde) \rVert on average, near the data \E_{\Xtilde \sim \SS} \left( \lVert \nabla_{\Xtilde} \fpsi(\Xtilde) \rVert - 1 \right)^2, \quad \SS \text{ between } \PP \text{ and } \Qtheta
  • Specifically: \Xtilde = \theta \X + (1 - \theta) \Y , \theta \sim \mathrm{Uniform}([0, 1])

Solution 2: add noise

  • Make the problem harder so there's no perfect discriminator
  • Use \X + \varepsilon , \Y + \varepsilon' for some independent, full-dim noise \varepsilon
  • But…how much noise \varepsilon to add? Also need more samples.
  • If \varepsilon \sim \mathrm{N}(0, \gamma I) and we take \gamma \to 0 , get \begin{gather} \gamma \E_{\PP}\left[ (1 - \Dpsi)^2 \lVert \nabla \log(\Dpsi) \rVert^2 \right] + \gamma \E_{\Qtheta}\left[ \Dpsi^2 \lVert \nabla \log(\Dpsi) \rVert^2 \right] \end{gather}
  • Same kind of gradient penalty!
  • Can also simplify to e.g. \gamma \E_{\X \sim \PP}\left[ \lVert \nabla \Dpsi(\X) \rVert^2 \right]

Solution 3: Spectral normalization [Miyato+ ICLR-18]

  • Regular deep nets: f_\ell = \sigma\left( W_\ell f_{\ell - 1}(x) + b_\ell \right)
  • Spectral normalization: f_\ell = \sigma\left( \frac{1}{\lVert W_\ell \rVert_2} W_\ell f_{\ell - 1}(x) + b_\ell \right)
  • \lVert W \rVert_2 := \sup_{x \ne 0} \frac{\lVert W x \rVert_2}{\lVert x \rVert_2} = \sigma_{\mathrm{max}}(W) is the spectral norm
  • Guarantees ^* \lVert f \rVert_\lip \le 1
  • Faster to evaluate than gradient penalties
  • Not as well understood yet

New samples [Mescheder+ ICML-18]

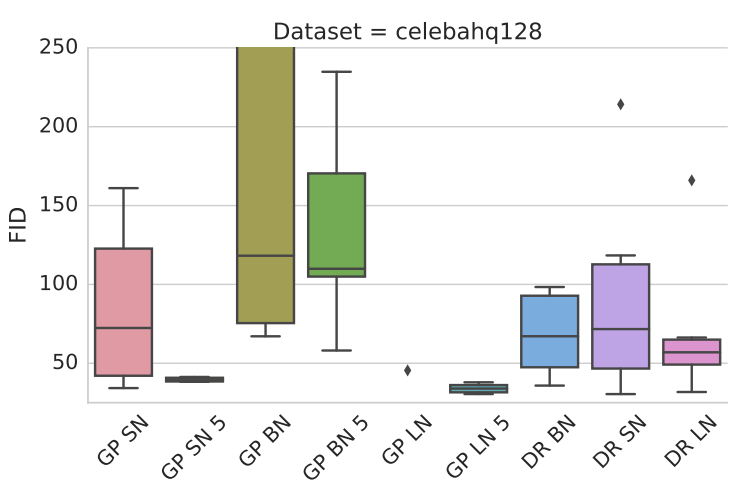
How to evaluate?

FID [Heusel+ NeurIPS-17] and KID [Bińkowski+ ICLR-18]

  • Consider distance between distributions of image features
  • Features \phi(x) from a pretrained ImageNet classifier
  • FID: \lVert \mu_\PP - \mu_{\Qtheta} \rVert^2 + \operatorname{Tr}\left( \Sigma_\PP + \Sigma_{\Qtheta} - 2 \left( \Sigma_\PP \Sigma_{\Qtheta} \right)^{\frac12} \right)
    • Estimator very biased, small variance
  • KID: use Maximum Mean Discrepancy instead
    • Similar distance with unbiased, ~normal estimator!

Comparing approaches [Kurach+ ICML-19]

Maximum Mean Discrepancy

\MMD(\PP, \QQ) = \sup_{f : \lVert f \rVert_{{\mathcal H}_k} \le 1} \E_{\X \sim \PP}[f(\X)] - \E_{\Y \sim \QQ}[f(\Y)]

\lVert f \rVert_{\mathcal{H}_k} is smoothness induced by kernel k : \dom \times \dom \to \R

Optimal f analytically: f^*(t) \propto \E_{\X \sim \PP} k(t, \X) - \E_{\Y \sim \QQ} k(t, \Y)

Estimating MMD

\begin{gather} \MMD_k^2(\PP, \QQ) % = \E_{\substack{\X, \Xp \sim \PP\\\Y, \Yp \sim \QQ}}\left[ % k(\X, \Xp) % - 2 k(\X, \Y) % + k(\Y, \Yp) % \right] = \E_{\X, \Xp \sim \PP}[k(\X, \Xp)] + \E_{\Y, \Yp \sim \QQ}[k(\Y, \Yp)] - 2 \E_{\substack{\X \sim \PP\\\Y \sim \QQ}}[k(\X, \Y)] \\ \fragment[0]{ \MMDhat_k^2(\X, \Y) = \fragment[1][highlight-current-red]{\mean(K_{\X\X})} + \fragment[2][highlight-current-red]{\mean(K_{\Y\Y})} - 2 \fragment[3][highlight-current-red]{\mean(K_{\X\Y})} } \end{gather}

K_{\X\X}

1.00.20.6
0.21.00.5
0.60.51.0

K_{\Y\Y}

1.00.80.7
0.81.00.6
0.70.61.0

K_{\X\Y}

0.30.10.2
0.20.30.3
0.20.10.4

MMD models [Li+ ICML-15, Dziugaite+ UAI-15]

  • No need for a discriminator – just minimize \MMDhat_k !
  • Continuous loss

Generator ( \Qtheta )

Critic

Target ( \PP )

How are these?

Not great! \MMDhat(\Qtheta, \PP) = 0.75

:( I'll try harder…

⋮

MMD models [Li+ ICML-15, Dziugaite+ UAI-15]

MNIST, mix of Gaussian kernels


\PP

\Qtheta

Celeb-A, mix of rational quadratic + linear kernels


\PP

\Qtheta

MMD loss with a smarter kernel

k(x, y) = \ktop(\phi(x), \phi(y))
  • \phi : \dom \to \R^{2048} from pretrained Inception net
  • \ktop simple: exponentiated quadratic or polynomial

\PP

\Qtheta

We just got adversarial examples!


[anishathalye/obfuscated-gradients]

Optimized MMD: MMD GANs [Li+ NeurIPS-17]

  • Don't just use one kernel, use a class parameterized by \vpsi : k_\vpsi(x, y) = \ktop(\phi_\vpsi(x), \phi_\vpsi(y))
  • New distance based on all these kernels: \optMMD(\PP, \QQ) = \sup_{\vpsi \in \vPsi} \MMD_{\vpsi}(\PP, \QQ)
  • Turns out that \optMMD isn't continuous: have \Qtheta \to \PP but \optMMD(\Qtheta, \PP) \not\to 0
  • Scaled MMD GANs [Arbel+ NeurIPS-18] correct \optMMD with a gradient penalty to make it continuous

Why MMD GANs?

  • “Easy parts” of the optimization done in closed form
image/svg+xml

StyleGANs [Karras+ 2018]

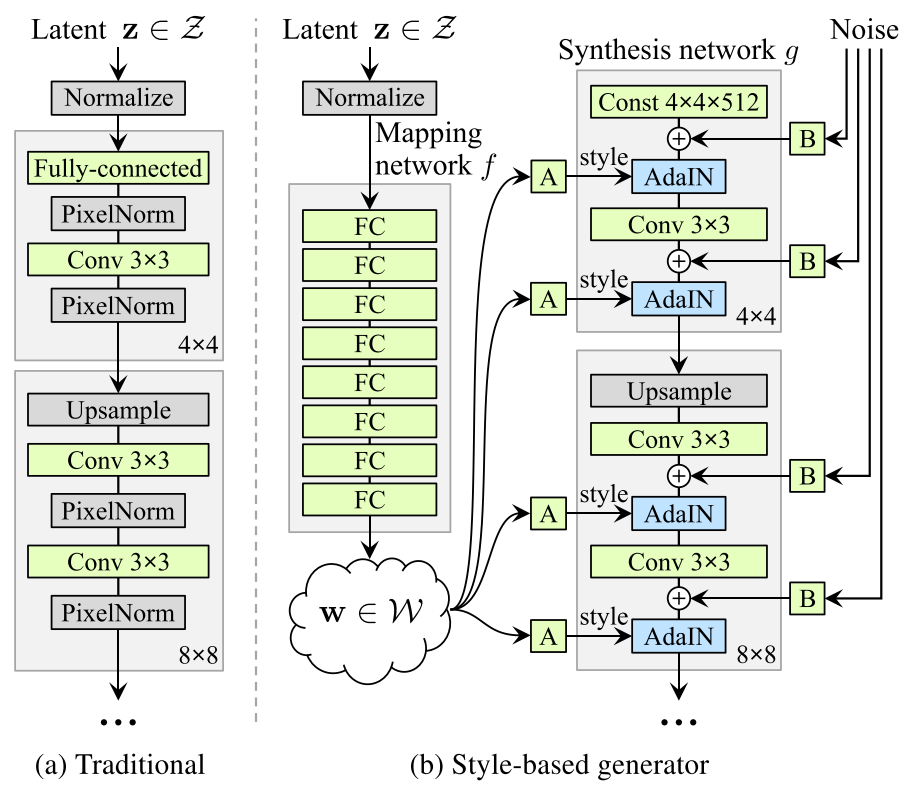
StyleGAN: latent structure

StyleGAN: local noise

StyleGANs on a different domain [@roadrunning01]

Finding samples you want [Jitkrittum+ ICML-19]

If we want to find “more samples like \{ \X \} ”:

\min_{\{ \Z_1, \dots, \Z_n \}} \MMDhat^2_k\left( \{ \X_i \}_{i=1}^m, \{ \Gtheta(\Z_i) \}_{i=1}^n \right)

Conditional GANs and BigGAN

  • Conditional GANs: [Mirza+ 2014]
    • Just add a class label as input to \Gtheta and \Dpsi
  • BigGAN [Brock+ ICLR-19]: a bunch of tricks to make it huge

Image-to-image translation [Isola+ CVPR-17]

Image-to-image translation [Isola+ CVPR-17]

CycleGAN [Zhu+ ICCV-17]

Pose-to-image translation [Chan+ 2018]

DeepFakes

Use your new knowledge for good!

Slides (including links to papers) are online:
dougal.me/slides/gans-mlcc