Evaluating and Training
Implicit Generative Models
with Two-Sample Tests

Dougal J. Sutherland
Gatsby unit, University College London

Implicit Generative Models workshop, ICML 2017

\DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\F}{\mathcal{F}} \newcommand{\h}{\mathcal{H}} \DeclareMathOperator{\mmd}{MMD} \DeclareMathOperator{\mmdhat}{\widehat{MMD}} \DeclareMathOperator{\N}{\mathcal{N}} \newcommand{\P}{\mathbb{P}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\target}{\text{target}} \newcommand{\test}{\text{test}} \newcommand{\train}{\text{train}} \DeclareMathOperator{\Var}{Var} \newcommand{\X}{\mathcal{X}} \newcommand{\Z}{\mathcal{Z}}

Implicit generative models

  • Given some samples from a distribution \P_\target on \X
  • Goal: generate more samples from \P_\target
  • Don't have an explicit likelihood model
[Gulrajani+ 2017]

Evaluating implicit generative models

  • Can't evaluate standard test-set likelihood
  • Early GAN papers: estimate this with KDE
  • KDE doesn't work in high d , theoretically or empirically
  • Models with high likelihoods can have terrible samples; those with good samples can have awful likelihoods [Theis+ ICLR-16]

Max-likelihood objective vs WGAN objective [Danihelka+ 2017]

Other evaluation methods

  • Birthday paradox test [Arora/Zhang 2017]
    • Needs a human
    • Only measures diversity
  • Inception score [Salimans+ NIPS-16]
    • Domain-specific
    • Only measures label-level diversity
  • …
  • Look at a bunch of pictures and see if they're pretty or not
    • Easy to find bad samples
    • Hard to see if modes missing, wrong probabilities
    • Hard to compare models

Two-sample tests

  • Given samples from two unknown distributions X \sim \P \qquad Y \sim \Q
  • Question: is \P = \Q ?
  • Hypothesis testing approach: H_0: \P = \Q \qquad H_1: \P \ne \Q

Applications of two-sample testing

  • Does my generative model \P_\theta match \P_\target ?
  • Do smokers/non-smokers have different cancer rates?
  • Do these neurons fire differently when the subject is reading?
  • Do these columns from different databases mean the same?
  • Independence: is P(X, Y) = P(X) P(Y) ?

General scheme for two-sample tests

  1. Choose some notion of distance \rho(\P, \Q)
    • Ideally, \rho(\P, \Q) = 0 iff \P = \Q
  2. Estimate the distribution distance from data: \hat\rho(X, Y)
  3. Say \P \ne \Q when \hat\rho(X, Y) > c_\alpha
    • Want (at least approximately) test of level \alpha : \Pr_{X, Y \sim \P}\left( \hat\rho(X, Y) > c_\alpha \right) \le \alpha
    • Test power is probability of true rejection: when \P \ne \Q , \Pr_{X \sim \P, Y \sim \Q}\left( \hat\rho(X, Y) > c_\alpha \right)

Mean difference

\rho(\P, \Q) = \lvert \E_\P \varphi(X) - \E_\Q \varphi(Y) \rvert \qquad \varphi(x) = x

Variance difference


\rho(\P, \Q) = \left\lVert \E_\P \varphi(X) - \E_\Q \varphi(Y) \right\rVert \qquad \varphi(x) = \begin{bmatrix} x \\ x^2 \end{bmatrix}

Higher-order differences

Need higher-order features still

Could keep stacking up moments, but get hard to estimate

Instead: use features \varphi : \X \to \h , for \h an RKHS

Refresher: Reproducing Kernel Hilbert Spaces

  • Using mean embedding \mu_\P = \E_\P \varphi(X)
  • \varphi : \X \to \h corresponds to kernel k(x, y) = \langle \varphi(x), \varphi(y) \rangle_\h
  • For any positive semidefinite k : \X \times \X \to \R , a matching \h and \varphi exist
    • e.g. k(x, y) = \exp\left( - \frac{1}{2 \sigma^2} \lVert x - y \rVert^2 \right)
  • Reproducing property: \forall f \in \h , f(x) = \langle f, \varphi(x) \rangle_\h

Maximum Mean Discrepancy

\begin{align} \mmd_k^2(\P, \Q) &= \left\lVert \mu_\P - \mu_\Q \right\rVert_\h^2 \\&\fragment{0}{ {} = \langle \mu_\P, \mu_\P \rangle_\h + \langle \mu_\Q, \mu_\Q \rangle_\h - 2 \langle \mu_\P, \mu_\Q \rangle_\h } \end{align}

\begin{align} \fragment{1}{\langle \mu_\P, \mu_\Q \rangle_\h} &\fragment{2}{{}= \E_{X, Y} \langle \varphi(X), \varphi(Y) \rangle_\h} \fragment{3}{{}= \E_{X, Y} k(X, Y)} \\&\fragment{4}{{}\approx \frac{1}{m n} \sum_{i=1}^n \sum_{j=1}^m k(X_i, Y_j)} \end{align}

\mmdhat_k^2 = \operatorname{mean}(K_{XX}) + \operatorname{mean}(K_{YY}) - 2 \operatorname{mean}(K_{XY})

Estimating MMD

\fragment{1}{\operatorname{mean}(K_{XX})} \fragment{2}{+ \operatorname{mean}(K_{YY})} \fragment{3}{- 2 \operatorname{mean}(K_{XY})}

1.00.60.50.20.40.2
0.61.00.70.40.10.1
0.50.71.00.30.10.2
0.20.40.31.00.70.8
0.40.10.10.71.00.6
0.20.10.20.80.61.0

MMD two-sample test

  1. Distance \mmd_k^2(\P, \Q) :
    • Need to choose a kernel k
    • For characteristic k , \rho_k(\P, \Q) = 0 iff \P = \Q
  2. Estimate the distance from data: \mmdhat_k^2(X, Y)
  3. Choose a rejection threshold c_\alpha
    • Use permutation testing to set \hat c_\alpha

Functional form of MMD

\begin{align} \mmd_k(\P, \Q) &= \lVert \mu_\P - \mu_\Q \rVert_\h \\&\fragment{0}{{}= \Big\lVert \E_{\P} \varphi(X) - \E_{\Q} \varphi(Y) \Big\rVert_\h} \\&\fragment{1}{{}= \sup_{f : \lVert f \rVert_\h \le 1} \left\langle f, \E_\P \varphi(X) - \E_\Q \varphi(Y) \right\rangle_\h} \\&\fragment{2}{{}= \sup_{f : \lVert f \rVert_\h \le 1} \E_\P \langle f, \varphi(X) \rangle_\h - \E_\Q \langle f, \varphi(Y) \rangle_\h} \\&\fragment{3}{{}= \sup_{f : \lVert f \rVert_\h \le 1} \E_\P f(X) - \E_\Q f(Y)} \end{align}

Form called integral probability metric

Maximizing function f called witness function (or critic)

Witness function

Witness function

Witness function

Witness function

Witness function

Witness function

The kernel matters!

The kernel matters!

The kernel matters!

Choosing a kernel

Choosing a kernel

Choosing a kernel

But how do we actually choose the kernel?

We want the most powerful test

Optimizing test power

  • Turns out a good proxy for asymptotic power is: \mmd^2(\P, \Q) / \sqrt{\Var_{X \sim \P, Y \sim \Q}\left[ \mmdhat^2(X, Y) \right]}
  • Can estimate this in quadratic time
  • …in an autodiff-friendly way

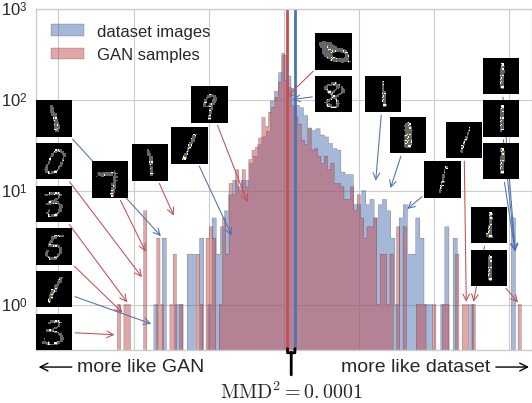
github.com/dougalsutherland/opt-mmd

Generative model criticism

Take a really good GAN on MNIST: [Salimans+ NIPS-16]


\P_\theta

\P_\target

Samples are distinguishable

ARD kernel on pixels: \exp\big( - \sum_{i=1}^d w_i (x_i - y_i)^2 \big)

p-values almost exactly zero

Investigating indicative points

Testing to generative modeling

  • Natural idea: train a generator G_\theta to minimize power of test
  • Consistent test, powerful generator class, infinite samples: \P_\theta \to \P_\target
  • Tradeoffs for unrealizable case depend on test

Integral probability metrics (IPMs)

\rho_{\F} = \sup_{f \in \F} \E_\P f(X) - \E_\Q f(Y)

Get different distances for different choices of \F :

  • f with \lVert f \rVert_\h \le 1 : MMD
  • f with \lVert f \rVert_\infty \le 1 : total variation
  • f that are 1-Lipschitz: Wasserstein
  • …

Classifier two sample tests (C2STs)

[Lopez-Paz/Oquab ICLR-17]

  • Let \F be set of functions \X \to \{0, 1\} : \rho_{\F}(\P, \Q) = \sup_{f \in \F} \left[ \E_\P f(X) - \E_\Q f(Y) \right] = 2 \, \text{acc} - 1
  • Estimator \hat\rho_{\F}(X, Y) :
  • Asymptotic power is monotonic function of \rho(\P, \Q)

Generative model based on C2STs

  • Train G_\theta to minimize C2ST power = accuracy of classifier
  • Accuracy hard to optimize, so use logistic surrogate
  • Envelope theorem: \nabla_x \sup_f f(x) = \nabla_x f^*(x)
  • Waste to retrain classifier each time: keep one discriminator
  • …and now we have a GAN

Generative Moment Matching Networks

[Li+ ICML-15], [Dziugate+ UAI-15]

  • Minimize \mmd_k(\P_\theta, \P_\target)
  • Samples are okay on MNIST
  • t -GMMN using test power instead: basically the same
  • Hard to choose a good kernel

Optimizing the kernel

Evaluating implicit generative models

  • One useful way is via two-sample-testing framework
  • MMD is a nice two-sample test, when you learn the kernel
  • Can help diagnose problems
  • More things to try for use on practical image problems

Training implicit generative models

  • Can define models based on power of two-sample tests
  • Might help with stability of training, etc

dougal@gmail.com
github.com/dougalsutherland/opt-mmd
Thanks!